Straw Man Fallacy of the Complete Conversation System Claim against the Turing Test

1. Introduction

In this paper, I argue that the well-known type of argumentation against the Turing test (TT) is aimed at something like an image (“straw man”) that is not in accordance with Turing’s idea. Following “Some historical remarks on Block’s ‘Aunt Bubbles’ argument,”¹ I will refer to the type of argument in question as the Complete Conversation System Claim (CCSC). Exemplary arguments of the CCSC type include the “Space Gramophone,”² “a dictionary-machine,”³ “Aunt Bubbles,”⁴ and “Chinese Room.”⁵ CCSC argumentation is constructed to show that the TT is not properly designed and, consequently, is not a good hallmark of intelligence. CCSC argumentation raises the following question: let us suppose that a machine passes the proposed test. Is this really evidence that it is intelligent, or should we rather say that it is only a bunch of tricks that enable the machine to pass the TT?

There have been previous attempts in the TT literature to inspect the connection between the test and the definition of intelligence. One should mention here Copeland’s critique of the “Chinese Room” and “Chinese Gym.” Copeland argues that the type of argumentation presented by Searle is “unsound and has no useful part to play in the discussion whether a symbol-processor can have intentionality.”⁶ Cole⁷ also addresses conceptual problems of the “Chinese Room” argument as a thought experiment (pointing, among other issues, to the disanalogy between the machine simulation of human performance and the human simulation of the machine). Along similar lines, Shieber⁸ analyzes the argumentation presented by Block⁹. By proposing a formal model of the test using the interactive proofs framework, Shieber’s argumentation aims “not to demonstrate that the Turing Test is sufficient as a criterion of intelligence. It merely shows that Block’s argument against its sufficiency fails.”¹⁰ My attempt in this paper is in line with the more general strategy described by Shieber, namely to show that CCSC argumentation against the TT “might be denigrated [...] on the grounds that Turing didn’t propose his Test as a criterion of intelligence.”¹¹ As such, it also has the merit of addressing the general structure of a group of arguments raised in the field of TT debates.

In what follows, I will describe the aforementioned arguments in detail and reconstruct the general schema of CCSC. After that, I will refer to the original ideas presented by Turing and his stance concerning the intelligence measured by the test in question. The last part of this paper addresses the question of the theoretical possibility of systems presented by CCSC in light of results discussed in “Turing interrogative games.”¹²

2. Complete Conversation System Claim

Let us start with a short description of the arguments listed in the Introduction. Stanisław Lem presents the argument which I will call “the Space Gramophone,” in his book Summa technologiae.¹³ Lem proposes the following thought experiment. Let us imagine a gramophone enlarged to the size of a planet (or “the Universe”). Now let us assume that the gramophone,

contains very many, say, one hundred trillion, recorded answers to all possible questions. And thus when we ask a question, the machine does not “understand” anything at all; it is only the form of the question, that is, the order of vibrations in our voice, that starts the transmitter which plays a record or tape containing a prerecorded answer. Let us not worry about technical details for now. It is obvious that such a machine will be inefficient, that no one is going to build it, because, first of all, this is not actually possible, but mainly because there is no need for it. Yet we are interested in the theoretical aspects of the problem.¹⁴

What is important is that the gramophone has complete conversations at its disposal: “Now, this is very difficult to program in advance, because it would mean the Designer of the ‘Cosmic Gramophone’ would have to record not only particular answers to possible questions but also whole sequences of conversations that can potentially take place.”¹⁵ And now the conclusion: “Given that it is behavior rather than internal design that determines whether a machine has consciousness, will this not make us jump to a conclusion that ‘the space gramophone’ does have consciousness – and thus talk nonsense (or rather pronounce untruth)?”¹⁶

Naturally, this argument is rather short and more of a sketch, but the idea presented is straightforward. The hypothetical machine in question has at its disposal a program that may be called the complete conversation system – a program that has answers to all possible questions. All that is needed is to recognize the question (by its form, not meaning) and then to choose one of the already prepared answers.

A short argument along these lines is also proposed by Shannon and McCarthy¹⁷ in the Preface to the Automata Studies. We read there:

A disadvantage of the Turing definition of thinking is that it is possible, in principle, to design a machine with a complete set of arbitrarily chosen responses to all possible input stimuli [...]. Such a machine, in a sense, for any given input situation (including past history) merely looks up in a “dictionary” the appropriate response. With a suitable dictionary such a machine would surely satisfy Turing’s definition but does not reflect our usual intuitive concept of thinking.¹⁸

Here, the gramophone is replaced by a machine equipped with a dictionary of appropriate responses. Again, technical details are not as important here as the theoretical implications – such a machine will pass the TT. However, we know that the success is due to purely automatic operations and “does not reflect our usual intuitive concept of thinking.” As noted by Copeland,¹⁹ the objection formulated above was rediscovered by a number of philosophers. In what follows, we take a closer look at the formulations proposed by Block and Searle.

In “Psychologism and Behaviorism”²⁰ (and later in “The Mind as the Software of the Brain”²¹), Ned Block proposes a more sophisticated and well-elaborated argument, which has the same analogous structure and aim as the ones presented by Lem and Shannon and McCarthy. It is known as the “Aunt Bubbles” argument. Block begins by establishing an upper limit of the duration of the TT, proposing for simplicity that it lasts 1 hour. He then suggests that we imagine a complete conversation tree containing all possible hypothetical conversations that last at most 1 hour. This is construed in a step-by-step fashion. In an idealized procedure, programmers would first write all strings of characters that may be typed within an hour or less, represented as A1,…,An. In the next step, they would find sensible responses to all A’s and list them as B1,...,Bn. Subsequently, they would list all possible replies to all B’s (represented as C with appropriate indices). The next task would be to produce possible machine responses to the C’s (just one for each of the C’s). This process would continue iteratively until all possible conversations of this 1-hour-long TT are accounted for – see Figure 1. Now, we just have to assume that there may exist a hypothetical machine with a storage capacity big enough to store the entire conversation tree.²²

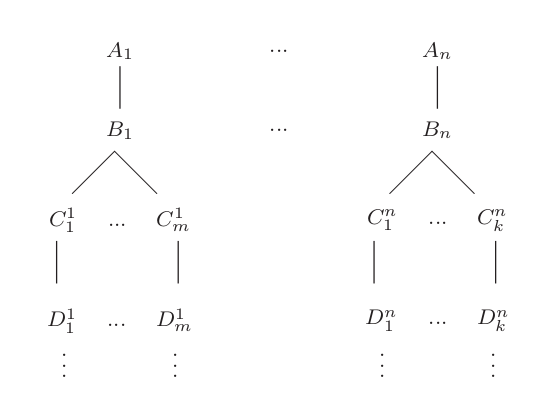
Each TT instance may be imagined as a path in this complete conversation tree. Each test starts with a judge asking one of the A’s, let us say Ai (“Whatever the judge types in [typos and all] is one of A1, ...,An”²³). The machine recognizes the question as Ai and replies with Bi (i.e., the predefined answer to Ai), and so on. This kind of machine may pass the TT easily because for each judge’s input, it has a predefined and relevant output in the complete conversation tree. The argument is longer and more detailed than the “Space Gramophone” or “the dictionary-machine,” but they certainly share the main assumptions and ideas.

One may find a clear analogy in Searle’s “Minds, Brains, and Programs”²⁴ and the “Chinese Room” argument. Searle writes: “Suppose that I’m locked in a room and given a large batch of Chinese writing. Suppose furthermore (as is indeed the case) that I know no Chinese, either written or spoken and that I’m not even confident that I could recognize Chinese writing as Chinese writing distinct from, say, Japanese writing or meaningless squiggles.”²⁵ Next, a second batch of symbols and a book of code are introduced to the room. The rules in the code book are written in English, and they show how symbols from the first batch correlate with the symbols in the second batch. This is done only on the basis of the form of the symbols without any knowledge of their meaning. Then Searle writes: “Suppose also that after a while I get so good at following the instructions for manipulating the Chinese symbols and the programmers get so good at writing the programs that from the external point of view that is, from the point of view of somebody outside the room in which I am locked – my answers to the questions are absolutely indistinguishable from those of native Chinese speakers. Nobody, just looking at my answers, can tell that I don’t speak a word of Chinese.”²⁶ Such a system may easily pass the TT. Here, the analogy of the complete conversation system is the book of code, which is used to generate plausible answers. As in the case of the “Space Gramophone” and the “Aunt Bubbles” arguments, questions are recognized only on the basis of their form (without understanding), and all the responses are already coded in the book.

The heart of the CCSC argumentation is the hypothetical solution, which ensures that a machine can recognize a question by its form and then match the relevant response from a prepared list. In the case of the “Space Gramophone,” such a solution is the database of responses stored by the device; for a machine described by Shanon and McCarthy, it is the dictionary of appropriate responses; for the “Aunt Bubbles” machine, the mechanism is encoded in the form of a tree; and for the “Chinese Room,” the responses are stored in a book of codes. Each machine, for an external observer, is indistinguishable from other people based on the answers provided. CCSC arguments share the same question: suppose that a described hypothetical machine (gramophone, dictionary-machine, Aunt Bubbles, or the room) passes the TT – and due to the construction of the machine, that will certainly happen. Is this really evidence that the machine is intelligent, or should we rather say that it is only a bunch of tricks enabling it to pass the TT?

CCSC argumentation points out that the concept of intelligence provided by the TT is wrong. As Block puts it, “the problem with the Turing test for theoretical purposes is that it focuses on performance rather than on competence. Of course, performance is evidence for competence, but the core of our understanding of the mind lies with mental competence, not behavioral performance.”²⁷ Searle also makes it clear that the TT offers the wrong definition of intelligence. “Since appropriately programmed computers can have input-output patterns similar to those of human beings, we are tempted to postulate mental states in the computer similar to human mental states. [...] The Turing test is typical of the tradition in being unashamedly behavioristic and operationalistic [...].”²⁸

As stated in the Introduction, I find this argumentation to be aimed at an image of the TT, not the test actually proposed by Turing. In what follows, I argue for this claim by examining Turing’s ideas and considerations about the TT and intelligence.

3. Turing Test

When discussing the TT, we encounter a phenomenon described by Gonçalves as “the Turing Test Dilemma.”²⁹ This dilemma draws attention to the fact that, despite many years of debate, it remains unclear whether the TT constitutes a valuable experiment for artificial intelligence (AI). This uncertainty arises because the test can be reconstructed in various ways. One approach focuses on reconstructing the rules of the game. This approach may be found, for example, in the aforementioned Shieber’s analysis of the TT as the interactive proof³⁰ (and is crucial for other formal models of the test, such as the one presented below). Also, Sterrett³¹ argues that we should focus on the “Original Imitation Game” Test involving three players³². Other interesting approaches are proposed by Gonçalves³³ and by Danziger³⁴. Gonçalves aims to shed light on the apparent lack of clarity in Turing’s 1950 paper by reconstructing the wider context for the emergence of the TT. This includes historical debates on the mind–machine controversy in England³⁵ and a persuasive reconstruction of the TT as a deliberately planned thought experiment (“had Turing been aware of it or not.”³⁶). This approach leads to the following conclusion:

In light of Mach’s analysis, Turing’s exposition of his various limitation tests should not be confused with loose rhetoric. Rather than being sloppy, the presentation of his thought experiments can now be understood as methodical. The various questions that Turing asked offered an empirical basis for discussing the original question (can machines think?) under varied limiting conditions. The design of his imitation game was deliberately flexible to address conceptual problems.³⁷

Danziger proposes yet another approach that highlights the socio-technological context of the TT. According to this idea, intelligence is perceived as a social concept, and what is crucial for a given entity to possess intelligence is its society’s attitude towards this entity. As Danziger argues:

Turing’s view implies that in a society holding a prejudiced, chauvinistic attitude toward machinery, machines cannot be perceived as intelligent entities, by definition. However, if such a society underwent a process in which its a priori attitude toward machinery changed, intelligent machines would become a logical possibility. [...] For Turing, the imitation game is not a test for intelligence, but a technological aspiration whose realization may involve a change in society’s attitude toward machines.³⁸

There is no need to present here a full reconstruction of the TT or to decide which of the approaches mentioned above should become the standard for future debates about the TT. In what follows, I will focus on several aspects of the test that are crucial for discussing CCSC argumentation. For this, the main source, “Computing Machinery and Intelligence,”³⁹ will be supplemented with the following ones: “Intelligent Machinery”⁴⁰; “Can Digital Computers Think”⁴¹; “Intelligent Machinery, a Heretical Theory”⁴²; “Can Automatic Calculating Machines be Said to Think?”⁴³; and “Digital Computers Applied to Games.”⁴⁴

Firstly, it should be stressed that the TT was meant to be of a statistical character and should be repeated several times for one agent to gain more reliable results.⁴⁵ Turing himself emphasized this point in a radio interview from 1952:

We had better suppose that each jury has to judge quite a number of times, and that some-times they really are dealing with a man and not a machine. That will prevent them saying “It must be a machine” every time without proper consideration.⁴⁶

The test for machines is rooted in the idea of imitation explored by Turing in the mathematical domain (Turing Machines, TM) and his experimentation with playing games. Imitation of one TM by another TM involves not copying its internal structure, but rather imitating its functions. Understanding this concept more broadly leads to the idea of imitating the functions of the human brain rather than its internal structure.

The important thing is to try to draw a line between the properties of a brain, or of a man, that we want to discuss, and those that we don’t. To take the extreme case, we are not interested in the fact that the brain has the consistency of cold porridge. We don’t want to say, “This machine’s quite hard, so it isn’t a brain, and so it can’t think.”⁴⁷

We can identify not only a prototype for the TT (i.e., the “paper chess machine” described in 1948), but also find traces of active experimentation with this prototype.⁴⁸

It is possible to do a little experiment on these lines, even at the present stage of knowledge. It is not difficult to devise a paper machine which will play a not very bad game of chess. Now get three men as subjects for the experiment A, B, C. A and C are to be rather poor chess players, B is the operator who works the paper machine. [...] Two rooms are used with some arrangement for communicating moves, and a game is played between C and either A or the paper machine. C may find it quite difficult to tell which he is playing. (This is a rather idealized form of an experiment I have actually done).⁴⁹

This tested idea is then coined into the proposal we know as the TT.

Now, we may ask whether the imitation of functions, according to Turing, should be seen as an operationalization of intelligence. Did he intend the test as a sort of definition, which is to be attacked by the CCSC?

Turing begins “Computing Machinery and Intelligence” by posing the question of whether machines can think. He soon concludes that this question is “too meaningless to deserve discussion.”⁵⁰ The reason for this is the lack of a widely accepted definition of thinking that could easily apply to machines.⁵¹ This is where the idea of imitation, stemming from the schema known from the “paper chess machine,” comes into play.

We now ask the question, “What will happen when a machine takes the part of A in this game?” Will the interrogator decide wrongly as often when the game is played like this as he does when the game is played between a man and a woman? These questions replace our original, “Can machines think?”⁵²

What will be evaluated is a machine’s behavior – its resemblance to human behavior in a similar situation – not the internal structure of the machine.

Turing clearly intended to avoid the discussion about thinking machines and instead focused on a clear criterion: the machine’s performance in a specified game. One might then ask how the results of such tests should be interpreted. Was Turing advocating the idea that a positive test result indicates the machine is intelligent? The first suggestion comes from a radio presentation by Turing entitled “Intelligent Machinery, a Heretical Theory,” in which he stated:

My contention is that machines can be constructed which will simulate the behavior of the human mind very closely. They will make mistakes at times, and at times they may make new and very interesting statements, and on the whole the output of them will be worth attention to the same sort of extent as the output of a human mind.⁵³

Machines simulating the human mind will be “worth attention,” just as the outputs of human minds are. Turing is not simply stating that those machines should be called intelligent. He made this even clearer in a radio interview from 1952 titled “Can Automatic Calculating Machines Be Said to Think?” After a brief presentation of the TT, he said:

Well, that’s my test. Of course, I am not saying at present either that machines really could pass the test, or that they couldn’t. My suggestion is just that this is the question we should discuss. It’s not the same as “Do machines think,” but it seems near enough for our present purpose, and raises much the same difficulties.⁵⁴

Discussing a machine’s performance in the test is not the same as discussing its intelligence. Turing points out that the issue of whether a machine passes the test or not is interesting in itself (“for present purpose”) and raises issues and problems to solve, even without considering the idea of intelligence.

In the subsequent part of the interview, he emphasizes this point even stronger:

I don’t want to give a definition of thinking, but if I had to I should probably be unable to say anything more about it than that it was a sort of buzzing that went on inside my head. But I don’t really see that we need to agree on a definition at all. The important thing is to try to draw a line between the properties of a brain, or of a man, that we want to discuss, and these that we don’t.⁵⁵

Until we agree on a definition of thinking (and as suggested in “Computing Machinery and Intelligence,” the concept should be suitable for use with machines⁵⁶), we should avoid interpreting success in the test as intelligence or treating such a successful machine as a thinking machine. Turing is aware that a reference to intelligence comes naturally, which is why he suggests that to avoid such a misleading conclusion, we may refer to these machines as “Grade A machines.”

I would like to suggest a particular kind of test that one might apply to a machine. You may call it a test to see whether the machine thinks, but it would be better to avoid begging the question, and say that the machines that pass are (let’s say) Grade A. machines.⁵⁷

A classical typology of intelligence from psychology, as described by D. O. Hebb, may be useful here. Hebb identified three types of intelligence: A, B, and C.⁵⁸ Intelligence A is the basic potentiality of the organism, whether animal or human, to learn and to adapt to its environment. It is determined by the organism’s genes but is mediated mainly by the complexity and plasticity of its central nervous system. Intelligence B is the level of ability that a person actually shows in behavior-cleverness, the efficiency and complexity of perceptions, learning, thinking, and problem-solving. This is not genetic. Rather, it is the product of the interplay between genetic potentiality and environmental stimulation. Intelligence C stands for the score obtained from a particular test. I would argue that CCSC aims to critique the TT as an operational definition of A or B type intelligence. In contrast, Turing’s intention, as I interpret it, was to capture type C intelligence – a specific class of machines capable of passing the imitation game. Therefore, CCSC argumentation appears to target a somewhat distorted portrayal (a “straw man”) of the TT.

The following quote sums this up nicely: “Most of the literature on Turing is written by logicians or philosophers who are often more interested in current philosophical questions than in Turing’s ideas.”⁵⁹ I like the quote because it also points out that the straw man fallacy of CCSC is important when we try to aim it specifically against the TT. If one attempts to dismiss or dispute strong AI – or, more generally, the computational model of mind – CCSC may become handy. One obstacle would be, however, the argument presented in the next section.

One last remark here would be to address the claims raised on the basis of CCSC argumentation – the “unashamedly behavioristic and operationalistic” character of the TT (as phrased by Searle). I would argue that this is exactly how the TT was meant to be, and it should not be considered a disadvantage. In light of the still-growing body of literature on the TT, one might question whether any superior alternatives to the input–output test (like the TT) have been proposed. A solution that offers criteria that are possible to use in practice. I would say that attempts aimed at replacing the TT with more sophisticated solutions – like Total Turing Test⁶⁰; Truly Total Turing Test,⁶¹ or the Lady Lovelace Test⁶² – are far from being a performable test due to the criteria of their use.⁶³ CSCC offers only a negative solution here without providing any positive one. I believe that this is what Turing predicted when he spoke about the difficulties raised by considering the rephrased questions about machines that he proposed.

4. Is there a trap in CCSC?

Łupkowski and Wiśniewski⁶⁴ introduce the concept of a Turing Interrogative Game (TIG for short). TIG is a special case of the TT, for which certain strict conditions are met. As it is argued in the paper, “once a TIG is performed, an instance of TT takes place.”⁶⁵ A TIG is introduced to explore the TT as a form of question–answer system, and the argumentation uses tools and results from the logic of questions⁶⁶ and recursion theory.⁶⁷ In what follows, I will briefly present the TIG rules and their consequences to CCSC.

A TIG is played by two parties: Int (after “Interrogator”) and M (after “Machine”). As in the TT, the role of Int is to ask questions, whereas M is supposed to answer them (and is not allowed to ask questions). What is novel here is the openly expressed requirement for a condition formulated by Int for each question asked. M is required to provide an answer that is correct with respect to the condition just set by Int.⁶⁸ “Correct” here does not presuppose that the answer is true, but means “resolving in view of the condition.”⁶⁹ There are no restrictions to the choice of questions and conditions by Int.

A TIG is played in rounds. In a round, Int sets a condition c and asks a question Q. M is supposed to provide an answer to Q that is correct with respect to c. The number of rounds of a TIG is always finite; however, there is no upper limit on the number of rounds that pertain to all TIGs: the games are unrestricted. It is up to Int to decide when the game ends.

Now, we may specify when M wins a round of TIG. To do this, M has to provide a certain expression that is a correct answer to the question asked with regard to the condition set; otherwise, M loses the round, and Int wins the round. Int loses a round if M wins the round. Observe that M can lose a round in two ways: (a) the expression provided is not an answer of the required kind, or (b) no output is provided. Int wins the game if and only if there is a round of the game that is lost by M; otherwise, Int loses the game, and M wins the game. M loses the game if M loses a round of the game.

TIGs aim to grasp the test as a form of question–answer system. Thus, the following assumptions about the language are accepted: (i) the set of expressions of the language includes declarative sentences (Phi) and questions (Psi); moreover, the # symbol occurs in the language; (ii) there exists a coding method according to which each expression is coded by a unique natural number; (iii) the set of sentences of the language is denumerable (countably infinite) and at least recursively enumerable (r.e. for short); and (iv) the set of questions of the language is r.e.

Several assumptions concerning answers are also made. Firstly, for each question Q and each condition c there exist(s) some (one or more) correct answer(s) to Q with respect to c. Secondly, any answer to Q that is correct with respect to some condition(s) is either a direct answer⁷⁰ to Q or a sentence that says “there is no correct answer” – in what follows written as #.

M is a machine, and thus, we expect that it will operate on the basis of a question-resolving (qr) algorithm. This qr-algorithm is a partial recursive function phi such that its domain dom(phi) is a subset of the cartesian product of Phi and Psi, and for any question Q and its condition c from the function domain, phi returns the correct answer to Q with respect to c.

A qr-algorithm phi is accessible to M if M is able to compute the values of phi for the whole domain of phi. The class of qr-algorithms that are accessible to M is non-empty and finite. As Łupkowski and Wiśniewski stress, “qr-algorithms do not define what is the correct answer in a given context; this is already preestablished.”⁷¹

This brings us back to CCSC. As pointed out above, at the core of each argument of this type lies a form of qr-algorithm – namely, an effective procedure that is able to produce a correct answer as the output for a given input. In the described cases, a machine is able to pass the TT with its qr-algorithm. The success of a machine is crucial for the “Space Gramophone,” “dictionary-machine,” “Aunt Bubbles,” and “Chinese Room.” It is the success of a machine that allows us to ask a question – whether we would agree that we may ascribe the success to machine intelligence.

Similarly, the success of a machine in a TIG seems to rely on which qr-algorithms are accessible to the machine. However, as Łupkowski and Wiśniewski argue, there are systematic reasons for which each machine loses some TIG(s). This effect is a phenomenon induced by the properties of the language in which a TIG is played.

Each TIG won by a machine, but played in a language in which there occurs at least one non-effective omega-question, has an extension which is won by the interrogator.⁷²

A question is called effective if and only if the set of (all the) direct answers to the question is non-empty and r.e. By an omega-question we mean a question whose set of direct answers is a denumerable (i.e., countably infinite) set of declarative sentences.

The proof of the presented proposition shows that no qr-algorithm is accessible to M that gives beta (an element of the set consisting of direct responses to Q and #) on an input consisting of Q and (any!) condition⁷³. On the other hand, the existence of such a beta is a consequence of a non-effective omega-question coming into play. The occurrence of a non-effective omega-question, in turn, is due to some general properties of the language in which a TIG is performed. It is enough for Int to extend a TIG to the point when a non-effective omega-question will be asked. M will lose a TIG instance by providing no output. Naturally, Int need not know in advance which question will trigger the effect – we allow for the unlimited number of TIG rounds, and the end of a TIG game is decided by Int.

Thus, generally speaking, if the game is played in a language that fulfills any of the above conditions, a machine always loses to an interrogator stubborn enough. This is the good news. But there is also the bad news: each machine loses, regardless of whether the machine thinks or not. This is The Trap.⁷⁴

It seems that The Trap identified here for TIGs is also present in CCSC argumentation. These arguments rely on the fact that a hypothetical machine passes the TT. For systematic reasons presented by Łupkowski and Wiśniewski, a machine operating on a qr-algorithm (analogous to the procedures described by Lem, Shannon with McCarthy, Block and Searle) is not able to win a TIG (which may be reasonably treated as an instance of the TT).

Naturally, CCSC arguments are thought experiments (as, to a large extent, an unlimited TIG instance is). However, it seems that these arguments rely on an idea that is wrong – the idea that we may somehow reach a complete question–answer system and an algorithmic procedure that always offers expected, relevant answers.

5. Summary

More than 70 years after its appearance, the TT is still present in academic (and not only academic) debates. I believe that the phenomenon of the TT’s popularity is beautifully explained by D. Dennett: “there are real world problems that are revealed by considering the strengths and weaknesses of the Turing test.”⁷⁵ Additionally, the boldness and simplicity of the proposal are important factors, in my opinion. However, I believe that sometimes these “real-world problems” blur the original idea of the test. Here, I can again refer to Dennett’s diagnosis:

It is a sad irony that Turing’s proposal has had exactly the opposite effect on the discussion of that which he intended. [...] He was saying [...] “Instead of arguing interminably about the ultimate nature and essence of thinking, why don’t we all agree that whatever that nature is, anything that could pass this test would surely have it; then we could turn to asking how or whether some machine could be designed and built that might pass the test fair and square.” Alas, philosophers – amateur and professional – have instead taken Turing’s proposal as the pretext for just the sort of definitional haggling and interminable arguing about imaginary counterexamples he was hoping to squelch.⁷⁶

The motivation for my paper comes from this observation. My contribution is to focus on Turing’s original proposal and to highlight his ideas behind the test in question. That is why I propose to identify an argumentation schema and refer to it as the Complete Conversation System Claim. I present four popular arguments aimed at the TT that fit this schema. Confronting CCSC argumentation with the original TT assumptions and Turing’s idea leads to the conclusion that CCSC commits the straw man fallacy. These arguments try to bring discussions concerning intelligence to the TT results – exactly what Turing himself intended to avoid by proposing the test.

The second part of the paper refers to the results concerning the completeness of the question–answer system. Here, I try to draw a connection to the algorithm that guarantees the success of the hypothetical machines presented in CCSC arguments.

I conclude that there are certainly benefits to presenting arguments of the CCSC type.⁷⁷ These thought experiments, appealing to our core intuitions about mechanistic ideas of thinking and human-like intelligence, inspire many fruitful debates. However, I would argue that each argument of this kind should be accompanied by two disclaimers. Firstly, they are not aimed at the TT as intended by Turing but rather at some interpretation of the test. Secondly, the core idea of the question-resolving algorithm of these hypothetical machines is also an idealization.